Redução polinomial e NP-completude

Como já foi dito, há muitos problemas de computação com aplicações práticas importantes para os quais não conhecemos algoritmos eficientes. Isto posto, uma ideia é investigar a complexidade relativa dos problemas em $\mathtt{NP}$ . Um problema $\mathcal A$ não é mais difícil que um problema $\mathcal B$ se uma solução para $\mathcal B$ implica numa solução para $\mathcal A$ com perda de desempenho polinomial relativa a eficiência da solução de $\mathcal B$ . Façamos isso mais preciso.

Se ${\mathcal A}$ e ${\mathcal B}$ são problemas computacionais de decisão então uma redução em tempo polinomial de ${\mathcal A}$ para ${\mathcal B}$ é um algoritmo eficiente ${M}$ que computa uma função ${M : \mathcal I(\mathcal{A}) \rightarrow \mathcal I(\mathcal{B})}$ tal que para todo instância ${I\in\mathcal I(\mathcal A)}$ de ${\mathcal A}$ a instância ${M(I)\in\mathcal I(\mathcal B)}$ do problema ${\mathcal B}$ têm a mesma resposta.

Escrevemos ${\mathcal A \leq_p \mathcal B}$ .

Notemos que se há uma redução de ${\mathcal A}$ para ${\mathcal B}$ e ${M_B}$ é um algoritmo que resolve ${\mathcal B}$ então o seguinte algoritmo resolve ${\mathcal A}$



 Devolva .

ademais, se ${M_B}$ é um algoritmo de tempo ${t(n)}$ e ${M}$ é um algoritmo de tempo ${p(n)}$ então ${M_A}$ acima tem consumo de tempo ${t(p(n))}$ , que é um polinômio sempre que ${t}$ for um polinômio. Notemos que ${|\langle M(I) \rangle| = O(p(|\langle I \rangle|))}$ , ou seja, a saída de ${M}$ tem tamanho polinomial no tamanho de ${I}$ . Com isso temos

Teorema 5 Se ${\mathcal A\leq_p \mathcal B}$ e ${\mathcal B \in \mathtt{P}}$ então ${\mathcal A \in \mathtt{P}}$ .

Teorema 6 ${\textsc{hamiltoniano} \leq_p \textsc{tsp}}$ .

Demonstração: Seja ${G=(V,A)}$ uma instância de ${\textsc{hamiltoniano}}$ . Considere o algoritmo que com entrada ${G}$ constrói o grafo ${K=(V,A')}$ completo sobre ${V}$ , constrói a função peso ${\rho : A \rightarrow \{1,2\}}$ dada por

$\displaystyle \rho ( \{x,y\} )= \begin{cases} 1, & \text{ se } \{x,y\}\in A\\ 2, & \text{ se } \{x,y\}\not\in A \end{cases}$

e toma ${k=|V|}$ .

Se ${G}$ é dado pela matriz de adjacências, ${\rho}$ é uma matriz obtida da matriz de ${G}$ trocando ${0}$ por ${2}$ . O grafo ${H}$ também e dado por uma matriz da mesma ordem. Assim, a descrição ${\langle H,\rho,k \rangle}$ é obtida em tempo linear de ${\langle G \rangle}$ .

Ainda, se ${G}$ tem um circuito hamiltoniano então ${H}$ tem um circuito hamiltoniano de peso ${k}$ . Se ${G}$ não tem um circuito hamiltoniano então todo circuito hamiltoniano de ${H}$ tem peso ${\geq k+1}$ . $\Box$

Um clique num grafo ${G}$ é um subconjunto de vértices que induz um subgrafo completo, isto é, todos os pares de vértices desse subconjunto são arestas no grafo. ${\textsc{clique}}$ é o problema: dado um grafo ${G}$ e um inteiro ${k>0}$ decidir se ${G}$ tem um clique com pelo menos ${k}$ vértices.

Uma cobertura num grafo ${G}$ é um subconjunto ${C}$ de vértices de ${G}$ tal que qualquer aresta de ${G}$ tem pelo menos um vértice em ${C}$ . ${\textsc{cobertura}}$ é o problema: dado um grafo ${G}$ é um inteiro ${k>0}$ decidir se ${G}$ tem uma cobertura com no máximo ${k}$ vértices.

Teorema 7 ${\textsc{clique} \leq_p \textsc{v\'ertice-cobertura}}$ .

Demonstração: Dada uma instância ${(G,k)}$ de ${\textsc{clique}}$ o algoritmo ${M}$ constrói em tempo linear ${\overline G}$ e toma ${|V|-k}$ para a instância ${(\overline G , |V|-k)}$ de ${\textsc{v\'ertice-cobertura}}$ . . Seja ${C}$ um clique com ${\geq k}$ vértices em ${G}$ . Então para toda aresta ${\{x,y\}}$ em ${\overline G}$ temos que como ${C}$ é independente em ${\overline G}$ no máximo um dentre ${x}$ e ${y}$ está em ${C}$ de modo que ${V-C}$ é uma cobertura em ${\overline G}$ com ${|V|-|C| \leq |V| - k}$ vértices.

Por outro lado, se ${D}$ é uma cobertura com no máximo ${|V|-k}$ vértices em ${\overline G}$ , então ${V-D}$ é independente em ${\overline G}$ , portanto, um clique com ${\geq k}$ vértices em ${G}$ $\Box$

Uma fórmula booleana satisfazível está em ${\textsc{3sat}}$ se todas as suas cláusulas têm exatamente 3 literais.

Teorema 8 ${\textsc{sat} \leq_p \textsc{3sat}}$ .

Demonstração: Seja ${\Phi=(X,C)}$ uma instância de ${\textsc{sat}}$ . Vamos descrever a construção de uma instância ${\Phi^{(3)}=(X^{(3)},C^{(3)})}$ de ${\textsc{3sat}}$ .

Seja ${C_i \in C}$ uma cláusula de ${\Phi}$ . A construção de ${\Phi^{(3)}}$ considera 4 casos de acordo com o número de literais da cláusula: ${1}$ , ${2}$ ${3}$ e ${\geq 4}$

Se ${|C_i|=1}$ , digamos que ${C_i = \ell_{i_1}}$ , então criamos a variáveis ${X_i^{(3)} = \{y_{i_2}, y_{i_3} \}}$ e escrevemos

$\displaystyle C_i^{(3)} := \bigg\{ \{ \ell_{i_1} , y_{i_2}, y_{i_3}\} , \{ \ell_{i_1} , \overline {y_{i_2}}, y_{i_3}\} , \{ \ell_{i_1} , y_{i_2}, \overline{ y_{i_3}}\},\{ \ell_{i_1} , \overline{y_{i_2}}, \overline{y_{i_3}}\} \bigg\}$

que corresponde à fórmula

$\displaystyle (\ell_{i_1} \vee y_{i_2} \vee y_{i_3}) \wedge (\ell_{i_1} \vee \overline {y_{i_2}} \vee y_{i_3}) \wedge (\ell_{i_1} \vee y_{i_2} \vee \overline { y_{i_3}}) \wedge (\ell_{i_1} \vee \overline {y_{i_2}} \vee \overline {y_{i_3}}) \ \ \ \ \ (4)$

Dessa forma, qualquer atribuição que faça ${ C_i^{(3)} }$ verdadeira, faz ${ C_i }$ verdadeira e qualquer extensão de uma atribuição que faça ${ C_i}$ faz ${ C_i^{(3)} }$ verdadeira.

Se ${|C_i|=2}$ , digamos que ${C_i =\{ \ell_{i_1}, \ell_{i_2}\}}$ , então criamos a variáveis ${X_i^{(3)} = \{y_{i_3} \}}$ e escrevemos

$\displaystyle C_i^{(3)} := \bigg\{ \{ \ell_{i_1} , \ell_{i_2}, y_{i_3}\} , \{ \ell_{i_1} , \ell_{i_2}, \overline{ y_{i_3}}\}\bigg\}$

que corresponde à fórmula

$\displaystyle (\ell_{i_1} \vee \ell_{i_2} \vee y_{i_3}) \wedge (\ell_{i_1} \vee \ell_{i_2} \vee \overline { y_{i_3}}) \ \ \ \ \ (5)$

Dessa forma, qualquer atribuição que faça ${ C_i^{(3)} }$ verdadeira, faz ${ C_i }$ verdadeira e qualquer extensão de uma atribuição que faça ${ C_i}$ faz ${ C_i^{(3)} }$ verdadeira.

Se ${|C_1|= 3}$ então ${X_i^{(3)} =\emptyset}$ e ${ C_i^{(3)} = C_i}$ .

Finalmente, se ${|C_1| = p > 3}$ , digamos que ${C_i = \{\ell_{i_1}, \ell_{i_2}, \dots , \ell_{i_p} \}}$ , então criamos as ${p-3}$ variáveis ${X_i^{(3)} = \{y_{i_1}, \dots, y_{i_{p-3}} \}}$ e fazemos ${ C_i^{(3)} }$ da seguinte forma

$\displaystyle \begin{array}{rcl} C_i^{(3)} =&\big\{ \{\ell_{i_1},\ell_{i_2},y_{i_1}\}, \\ &\{\overline{y_{i_1}},y_{i_2},\ell_{i_3}\}, \\ &\{\overline{y_{i_2}},y_{i_3},\ell_{i_4}\}, \\ &\{\overline{y_{i_3}},y_{i_4},\ell_{i_5}\}, \\ &\vdots \\ &\{\overline{y_{i_{p-3}}},\ell_{i_{p-1}},\ell_{i_p}\}\big\}. \end{array}$

e fica como exercício verificar que se ${ C_i}$ é satisfazível se, e só se, ${ C_i^{(3)}}$ é satisfazível. Com isso, a fórmula ${\Phi^{(3)}}$ é dada pelas variáveis ${X \cup (\bigcup_i X_i^{(3)})}$ e pelas cláusualas ${\bigcup_i C_i^{(3)}.}$ .

Resta mostrar que essa construção pode ser feita em tempo polinomial no tamanho da descrição de ${\Phi}$ . $\Box$

$\textsc{clique}$ é a linguagem definida pelo problema de decisão: Dado um grafo ${G}$ e um natural ${k}$ decidir se ${G}$ contém um clique com ${\geq k}$ vértices.

Teorema 9 ${\textsc{3sat} \leq_p \textsc{clique}}$ .

Demonstração: Seja ${\Phi = (X,C)}$ uma instância de ${\textsc{sat}}$ e vamos construir uma instância ${(G, |C|)}$ de ${\textsc{clique}}$ .

Se ${\Phi}$ tem cláusulas ${C_1,C_2,\dots,C_k}$ então ${G}$ tem ${3k}$ vértices denotados ${v_{i,j}}$ , para ${1\leq i \leq k}$ e ${1\leq j \leq 3}$ . O vértice ${v_{i,j}}$ corresponde ao literal ${j}$ da cláusula ${i}$ , denotado ${\ell_{i,j}}$ . As arestas são dadas pelos pares de vértices

$\displaystyle \{ v_{i,j} ,v_{k,l}\}$

com ${i\neq k}$ (correspondem a cláusulas diferentes) e cujos literais podem ser simultaneamente verdadeiros (não contraditórios). Notemos que ${C_i= \{\ell_{i,1}, \ell_{i,2},\ell_{i,3}\}}$ corresponde a um conjunto independente ${\{v_{i_1}, v_{i_2},v_{i_3}\}}$ em ${G}$ .

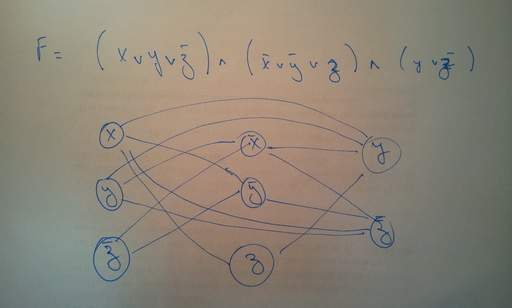
satclique

Seja ${t}$ uma atribuição que satisfaz todas as cláusulas de ${\Phi}$ e sejam ${\ell_{1,j_1},\dots,\ell_{k,j_k}}$ um literal com valor ${\textsc{verdadeiro}}$ de cada cláusula. Então ${v_{1,j_1},v_{2,j_j},\dots,v_{k,j_k}}$ é um clique com ${k}$ -vértices em ${G}$ .

Agora, suponha que ${G}$ tem um clique com pelo menos ${k}$ vértices. Seja ${U}$ um subconjunto de vértices de cardinalidade ${k}$ que define um clique em ${G}$ . Como vértices da mesma cláusula não são adjacentes, devemos ter um vértice correspondente a cada cláusula de ${\Phi}$ . Definimos a seguinte atribuição na variáveis de ${\Phi}$ : se ${x}$ é uma variável que corresponde a um vértice de ${U}$ então ${t(x)}$ é verdadeiro, caso contrário, ${t(x)}$ é falso. Assim ${t}$ satisfaz todas as cláusulas.

Resta mostrar que essa construção pode ser feita em tempo polinomial no tamanho da descrição de ${\Phi}$ . Basta notar que ${G}$ tem ${3k}$ vértices portanto construímos uma matriz de tamanho ${9k^2}$ que é polinomial no tamanho da representação de ${\Phi}$ . $\Box$

Exercício 5 ${\textsc{conjunto-independente}}$ é o problema: Dado um grafo ${G}$ e um natural ${k}$ decidir se ${G}$ contém um conjunto independente com ${\geq k}$ vértices. Prove que ${\textsc{3sat} \leq_p \textsc{conjunto-independente}}$ .

— NP-completude —

Um problema ${\mathcal A}$ é ${\mathtt{NP}}$ -difícil se todos os problemas em ${\mathtt{NP}}$ não são mais difíceis do que ${\mathcal A}$ no seguinte sentido:

$\displaystyle \mathcal B \leq_p \mathcal A \text{ para todo }\mathcal B \in \mathtt{NP}. \ \ \ \ \ (6)$

Suponhamos que ${\mathcal A}$ tenha um algoritmo ${M_{\mathcal A}}$ que o resolve em tempo ${O(n^t)}$ e seja ${M}$ a redução de ${\mathcal B\in\mathtt{NP}}$ para ${\mathcal A}$ que consome tempo ${O(n^k)}$ para algum natural ${k}$ . Então, se ${I}$ é uma instância de tamanho ${n}$ para ${\mathcal B}$ , ${M(I)}$ é uma instância de tamanho ${O(n^k)}$ para ${\mathcal A}$ cuja resposta ${M_{\mathcal A}( M(I))}$ é computada em tempo ${O( (n^k)^t )}$ . Portanto,

Teorema 11 Se algum problema ${\mathtt{NP}}$ -difícil tem algoritmo eficiente, todos os problemas em ${\mathtt{NP}}$ têm algoritmo eficiente, isto é, ${\mathtt{P}=\mathtt{NP}}$ .

Um problema é ${\mathcal A}$ ${\mathtt{NP}}$ -completo se

${\mathcal A\in \mathtt{NP}}$ ,
${\mathcal A}$ é ${\mathtt{NP}}$ -difícil.

Como consequência dessa definição e da proposição acima

Corolário 12 Se algum problema ${\mathtt{NP}}$ -completo tem algoritmo eficiente então ${\mathtt{P}=\mathtt{NP}}$ .

Proposição 13 Se algum problema ${\mathtt{NP}}$ -completo não tem algoritmo eficiente então nenhum outro problema ${\mathtt{NP}}$ -completo tem, isto é ${\mathtt{P}\cap \mathtt{NP-completo}=\emptyset}$ .

Demonstração: Exercício. $\Box$

Proposição 14 Se ${\mathcal A}$ é ${\mathtt{NP}}$ -completo e ${\mathcal A\leq_p \mathcal B}$ então ${\mathcal B}$ é ${\mathtt{NP}}$ -difícil.

Demonstração: Exercício. $\Box$

Teorema 15 (Cook e Levin, 1970) ${\textsc{sat}}$ é ${\mathtt{NP}}$ -completo.

Corolário 16 ${\textsc{3sat}}$ é ${\mathtt{NP}}$ -completo.

Demonstração: Vimos que ${\textsc{sat} \leq_p \textsc{3sat}}$ , portanto, ${\textsc{3sat}}$ é ${\mathtt{NP}}$ -difícil. Claramente, ${\textsc{3sat}}$ está em ${\mathtt{NP}}$ (por quê?). $\Box$

Corolário 17 ${\textsc{clique}}$ é ${\mathtt{NP}}$ -completo.

Demonstração: Vimos que ${\textsc{3sat} \leq_p \textsc{clique}}$ , portanto, ${\textsc{3sat}}$ é ${\mathtt{NP}}$ -difícil. Fica como exercício para o leitor verificar que ${\textsc{clique}}$ está em ${\mathtt{NP}}$ . $\Box$

Corolário 18 ${\textsc{v\'ertice-cobertura}}$ é ${\mathtt{NP}}$ -completo.

Demonstração: Vimos que ${\textsc{clique} \leq_p \textsc{v\'ertice-cobertura}}$ , portanto, ${\textsc{v\'ertice-cobertura}}$ é ${\mathtt{NP}}$ -difícil. Fica como exercício para o leitor verificar que ${\textsc{v\'ertice-cobertura}}$ está em ${\mathtt{NP}}$ . $\Box$

Além desses, dos outros problemas citados nestas notas, é sabido que ${\textsc{hamiltoniano}}$ é ${\mathtt{NP}}$ -completo e que ${\textsc{tsp}}$ é ${\mathtt{NP}}$ -completo. Uma curiosidade: em maio de 2004, o problema caixeiro-viajante nas 24.978 cidades da Suécia foi resolvido (veja aqui).

Há muitos problemas ${\mathtt{NP}}$ -completos. São tantos e tão pesquisados que muitos pesquisadores acreditam que ${\mathtt{P}\neq \mathtt{NP}}$ simplesmente porque se houvesse um algoritmo eficiente para algum desses problemas ele certamente já teria sido descoberto. Veja aqui uma lista de problemas ${\mathtt{NP}}$ -completos.

Notas de aula

Jair Donadelli

Redução polinomial e NP-completude

Deixe um comentário Cancelar resposta

Compartilhe isso:

Relacionado

Deixe um comentário Cancelar resposta